fereleo.blogg.se - Program for bisection method in fortran compilers

#Program for bisection method in fortran compilers how to#
#Program for bisection method in fortran compilers code#

Obviously it can handle an index of 0, but it's just not typical of Fortran programs.

Fortran is 1-indexed, so it's more natural in the language to use dimension(1:n) (or even dimension(n), which is the same thing as the other), instead of defining it as dimension(0:n).

Note that the interface block has the same structure as the declaration part of the subroutine, so it should be obvious that it is necessary for the inputs of the different functions to be the same, otherwise we'd have a compiler error. Subroutine rk4(n, h, x, nstep, sub, xout)

#Program for bisection method in fortran compilers how to#

I'm also going to snip out most of the code, as I don't think much is needed to show how to do it.

#Program for bisection method in fortran compilers code#

I'm going to go with the latter since it's easier here due to code size, but the strategy really isn't that different with using a module. The compiler also needs to be aware of the function/subroutine you are calling, which means either using a module to hold the RK4 subroutines or, with small enough code, a contains block. To pass a function or subroutine to another, you need to declare it with an interface block. ! calculate the solution to the boundary value broblemġ00 format (1x,I5,f10.2,f15.6,f15.6,f15.6) Real(8) :: V(nstep),out(nstep) ! V just like U for another equation

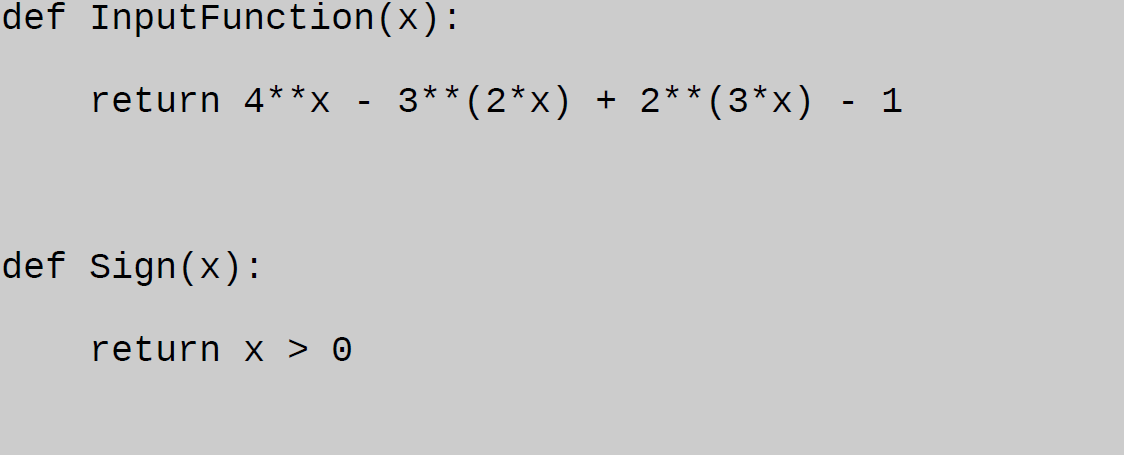
Real(8) :: U(nstep) ! U contains the solutions at each step ! and using Runge-Kutta method of order N = 4 ! To approximate the solution of boundary value problem I had to copy the rk4 subroutine for each equation of U and V. I have wrote a code to approximate the solution of a boundary value problem: x'' = p(t)x'(t)+q(t)x(t)+r(t)īy using Runge-Kutta method of order N = 4.ĭo you have any idea to make it short? I don't know how to call a subroutine as an argument in another subroutine.